Задача 3

Задача

Тело, неподвижно лежащее на поверхности Земли, участвует в ее вращательном движении. В момент времени t₀ Земля становится «прозрачной» для тела (то есть тело получает возможность двигаться сквозь Землю, не встречая сопротивления). Определить характер движения тела в последующие моменты времени (найти траекторию движения) для двух случаев:
1) тело первоначально находилось на экваторе;
2) тело находилось на широте . Землю считать однородным шаром.

Решение

1. Определим суммарную силу, действующую на тело.

Предположим, (а в дальнейшем мы это докажем) что тело все время движется внутри Земли. Пусть в данный момент времени тело находится на расстоянии r от центра Земли. Разобьем всю Землю на две области: шар радиуса r и внешнюю (по отношению к телу) сферическую оболочку (Рис.1).

Рис. 1

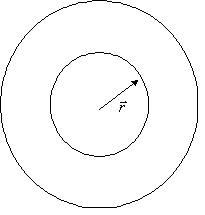
Суммарная сила, действующая на тело со стороны внешней сферической оболочки равна 0 (это является хорошо известным фактом, но может быть и доказано стандартными методами). Суммарная сила, действующая на тело со стороны шара, равна силе взаимодействия с материальной точкой, помещенной в центр шара и имеющей массу, равную массе шара (тоже хорошо известный результат). Таким образом,
,
где 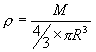- плотность Земли.

Окончательно получаем
            (1)

Здесь - гравитационная постоянная, M и R – масса и радиус Земли, соответственно.

2. Запишем уравнения движения.

Как видно из уравнения (1) на тело действует центральная сила. В этом случае момент импульса, равный

сохраняется, то есть движение будет происходить в экваториальной плоскости. Выберем начало отсчета в центре Земли, ось Y проведем через точку, занимаемую телом в момент времени t₀, ось X – перпендикулярно оси Y. Проектируя уравнение движения
  или  , где

на оси координат, получим систему уравнений

, где             (2)

то есть типичные уравнения колебательного движения, решения которых хорошо известны:

Произвольные постоянные A, B, и определяются из начальных условий:

, 
, 

(мы полагаем t₀=0). Здесь V₀– начальная скорость тела. Применяя приведенные равенства к решениям (2), получим

, , , ,  то есть

, .            (3)

Теперь легко получаем уравнение траектории

,

то есть уравнение эллипса, где A и B – его полуоси (центр эллипса расположен в начале координат).

Решения (3) справедливы только в том случае, если в течение всего времени движения тело остается внутри Земли (или на ее границе), так как мы полагали, что . Это условие будет выполнено, если справедливы соотношения A R и B R. Выполнение второго условия очевидно, а первое приводит к ограничению на начальную скорость точки:

  ,  или иначе ,
где - первая космическая скорость.            (4)

Отметим здесь два обстоятельства. Во-первых, при решении мы нигде не использовали тот факт, что тело покоится относительно Земли, так что оно годится и для движущегося относительно Земли тела. А во-вторых, V₀ - это скорость тела в инерциальной системе отсчета, то есть для покоящегося относительно Земли тела (на экваторе) , где - угловая скорость вращения Земли. Таким образом, условия (4) для нашего случая заведомо выполняются.

Теперь ответим на второй вопрос задачи. Этот случай отличается от предыдущего только тем, что начальный момент импульса тела (относительно центра Земли) имеет другое значение: , где -расположен под углом к плоскости экватора, а . Поскольку момент сохраняется, то движение будет происходить в плоскости, определяемой векторами и . Поэтому в системе координат , повернутой относительно системы так, что плоскость совпадает с указанной плоскостью, уравнения (3) будут иметь такой же вид. Поэтому все дальнейшие выводы также остаются в силе. Условия (4), разумеется, выполняются.