ОЛИМПИАДНОЕ ЗАДАНИЕ
2003 г.
1. На экваторе расположена башня высотой h, на вершине которой на нити подвешено тело. В некоторый момент времени нить перерезают и тело начинает падать. Восточнее или западнее основания башни и на каком расстоянии от него упадет тело. Влиянием атмосферы пренебречь. Решение (12 баллов)
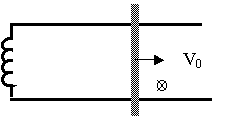 3. На двух гладких горизонтальных
параллельных рельсах, расстояние между которыми l, находится проводящая перемычка массой m. К рельсам подсоединена
катушка индуктивностью L. Однородное магнитное
поле индукцией B направлено вертикально.
Перемычке сообщают скорость V0
вдоль
рельс. На какое максимальное расстояние сможет удалиться перемычка от начального
положения? Решение (11 баллов)
3. На двух гладких горизонтальных
параллельных рельсах, расстояние между которыми l, находится проводящая перемычка массой m. К рельсам подсоединена
катушка индуктивностью L. Однородное магнитное
поле индукцией B направлено вертикально.
Перемычке сообщают скорость V0
вдоль
рельс. На какое максимальное расстояние сможет удалиться перемычка от начального
положения? Решение (11 баллов)
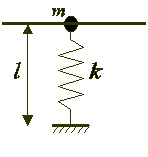
4. Найти молярную теплоемкость воздуха, находящегося внутри мыльного пузыря радиуса r. Поверхностное натяжение мыльной пленки s, атмосферное давление P0, молярная теплоемкость воздуха при постоянном объёме сv . Решение (8 баллов)
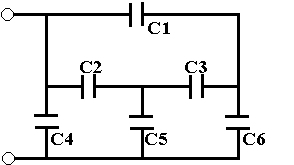 5. Найти емкость системы одинаковых
конденсаторов, изображенных на рисунке. Емкость конденсаторов С.
Решение (8 баллов)
5. Найти емкость системы одинаковых
конденсаторов, изображенных на рисунке. Емкость конденсаторов С.
Решение (8 баллов)