Решения

ЗАДАЧ ОБЛАСТНОЙ МЕЖВУЗОВСКОЙ ОЛИМПИАДЫ СТУДЕНТОВ ПО ФИЗИКЕ 2003 г.

Задача 1.

На экваторе расположена башня высотой h, на вершине которой на нити подвешено тело. В некоторый момент времени нить перерезают и тело начинает падать. Восточнее или западнее основания башни и на каком расстоянии от него упадет тело. Влиянием атмосферы пренебречь.

Решение.

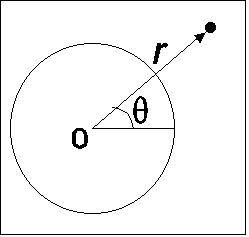Как хорошо известно, если потенциал зависит только от модуля r расстояния до силового центра, то движение тела происходит с сохранением момента импульса в плоскости, ортогональной . В плоскости экватора введем полярную систему координат , где r – расстояние до центра Земли, – полярный угол.

Уравнения движения имеют 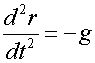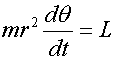вид , . Начальные условия имеют вид , , 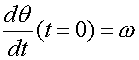где R – радиус Земли, – угловая частота вращения Земли. Первое уравнение дает

,

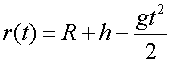откуда определяем время падения (условие ). Второе уравнение дает

.

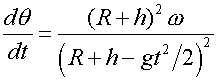За время полета угловое смещение тела равно

.

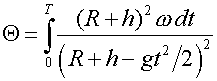По очевидным причинам 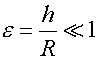. Разлагая подынтегральное выражение в ряд по , в линейном порядке имеем

.

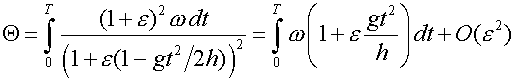Интегрирование дает 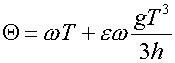. Основание башни за время падения сместится на угол . Расстояние от точки падения тела до основания башни равно

.

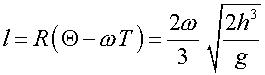Понятно, что тело упадет восточнее основания башни.

Задача 2.

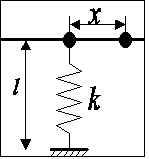Шарик массы m, без трения скользящий по прямолинейному горизонтальному стержню, упруго закреплен вертикальной пружиной с жесткостью k. В положении равновесия натяжение пружины отсутствует, и длина ее равна l. Как изменится период малых колебаний системы, если начальное отклонение от положения равновесия увеличить в 2 раза. (Указание: использовать интеграл движения энергию.)

Решение:

Пусть x – смещение от положения равновесия. Удлинение пружины равно а ее энергия .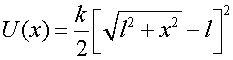

В случае малых колебаний, когда , разложим потенциальную энергию в ряд и ограничимся первым членом:

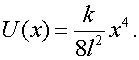
Таким образом, малые колебания этой системы оказываются нелинейными. Пусть A – начальное отклонение от положения равновесия (полуразмах колебаний), а T – период колебаний. Используя известное из механики соотношение

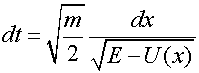
и учитывая равенство для энергии системы 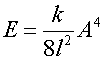, запишем выражение для полупериода

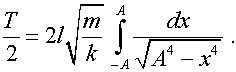
Переходя к безразмерной переменной , после элементарных преобразований получаем

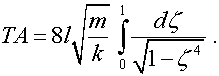
TA=const, и при увеличении A в 2 раза период уменьшается в 2 раза.

Задача 3

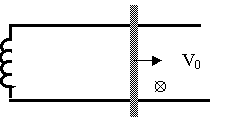На двух гладких горизонтальных параллельных рельсах, расстояние между которыми l, находится проводящая перемычка массой m. К рельсам подсоединена катушка индуктивностью L. Однородное магнитное поле индукцией B направлено вертикально. Перемычке сообщают скорость V₀ вдоль рельс. На какое максимальное расстояние сможет удалиться перемычка от начального положения?

Решение.

Сила Ампера (1)

ЭДС индукции (2)

Продифференцируем (1) по времени и подставим в (2) :

Получено дифференциальное уравнение гармонических колебаний с циклической частотой

Его решение с учетом начальных условий V=V₀ cosw t .

Для координаты

Максимальное расстояние, на которое сможет удалиться перемычка, есть амплитуда колебаний

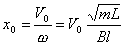
Задача - 4

Найти молярную теплоемкость воздуха, находящегося внутри мыльного пузыря радиуса r. Поверхностное натяжение мыльной пленки s, атмосферное давление P₀, молярная теплоемкость воздуха при постоянном объёме с_v .

Решение.

Сообщим воздуху количество теплоты dQ, его температура повысится на dT , радиус увеличится на dr. Первое начало термодинамики:

dQ=PdV+C_vdT ;

где приращение объёма и давления соответственно dV=4pr² dr,

Давление внутри пузыря

Из уравнения состояния PV=nRT следует PdV+VdP=nRdT, отсюда

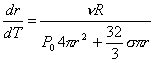
Окончательно молярная теплоемкость

Задача - 5 Найти емкость системы одинаковых конденсаторов, изображенных на рисунке. Емкость конденсаторов С.

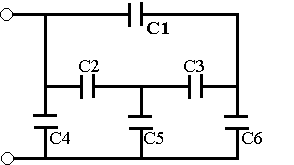
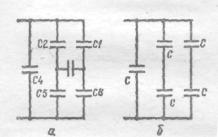
Решение

Схему удобно перерисовать так, как показано на рисунке а. Из симметрии схемы следует, что разность потенциалов пластин конденсатора С3 равна нулю. Следовательно, этот конденсатор не заряжен и может быть изъят (рис.б). Емкость получившейся системы найти уже легко. Она равна 2С.