Задача 5

Задача

Предположим, что с точки зрения наблюдателя О, покоящегося относительно далеких неподвижных звезд, распределение этих звезд изотропно. А именно, в любом телесном угле наблюдатель О видит звезд, где N - общее число звезд, доступных наблюдению. Пусть другой наблюдатель О' движется относительно первого с постоянной релятивистской скоростью . Ответьте на следующие вопросы.

• Какое распределение звезд увидит второй наблюдатель? Считая, что число звезд, видимых наблюдателем О' в телесном угле , равно , найти плотность распределения .
• Где второй наблюдатель увидит скопление звезд? Найдите значение такое, что половина всех звезд заключена в интервале .

Указание. Релятивистский закон сложения скоростей имеет вид

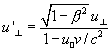, , где .

Решение

Введем в системе отсчета S, связанной с наблюдателем O, сферическую систему координат, в которой выделенное направление задается вектором . Если некоторая звезда имеет в этой системе радиус-вектор

,

.

Компонента скорости фотонов вдоль вектора равна . Аналогичным образом в сферической системе координат, которая связана с наблюдателем O' и в которой выделенное направление задается также вектором , продольная компонента скорости наблюдаемых фотонов равна . Используя формулу преобразования продольной компоненты, получаем соотношение

,

.

Из соотношения между косинусами следует, что

.

Кроме того, аксиальный угол . Тогда число звезд, наблюдаемых в телесном угле , равно

.

Поскольку , то в системе отсчета S', связанной с наблюдателем O', плотность распределения звезд

.

Это соотношение отвечает на первый вопрос. Далее, пусть . Из равенства

,

,
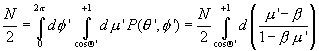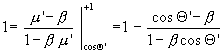