Задача 1

Задача. Дана бесконечная плоская проводящая сеть с квадратными ячейками. Сопротивление каждого прямолинейного проводника, соединяющего два ближайших узла, равно 1 Ом. Определить сопротивление между двумя соседними узлами сети.

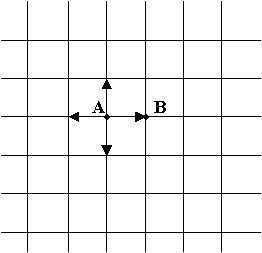
Решение. Решение этой задачи опирается на принцип суперпозиции и использование симметрии сети. Цепь постоянного тока из сопротивлений - линейная система, так как распределение потенциалов и токов в цепи подчиняется линейным уравнениям, выражающим правила Кирхгофа. Следовательно, если два данных распределения потенциалов и токов являются возможными состояниями цепи, то сумма этих распределений также будет возможным состоянием цепи. Рассмотрим следующие два распределения токов. Первое распределение возникает, если опустить в узел A электрод, с которого “стекает” ток I (см. рис.). Ввиду симметрии ток распределяется из узла A так, как показано на рис. (a), и из узла A в узел B идет ток I/4.

(a)

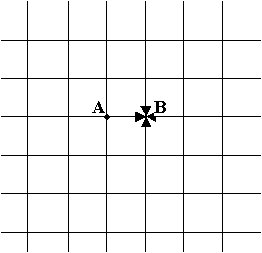
(b)

Второе распределение возникает, если опустить в узел B электрод с “обратным” потенциалом. Электрод будет “собирать” ток I, как показано на рис. (b), и из узла A в узел B идет ток I/4. Взяв суперпозицию двух описанных распределений токов, мы получаем третье возможное состояние цепи, в котором с одного электрода в узел A “втекает” ток I, другой электрод из узла В “собирает” ток I, а по отрезку AB из A в B идет ток I/4 + I/4 = I/2.

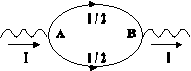
Вся остальная часть сети переносит из A в B ток I/2 и поэтому эквивалентна отрезку AB. Это можно изобразить следующей эквивалентной схемой.