Кафедра теоретической физики

Программа по курсу

Математический анализ

Семестp III

В программе математического анализа представлена теория числовых и функциональных рядов, включая ряды Фурье. Даны основы теории интеграла Фурье. Векторный анализ строится на основе алгебры тензоров. Подчеркивается инвариантный смысл дифференциальных операций векторного анализа, развита удобная техника дифференцирования векторных и скалярных полей. Доказываются основные интегральные теоремы векторного анализа. Обсуждаются приемы работы в ортогональных криволинейных системах координат.

Сходимость и сумма числового ряда. Критерий Коши. Необходимое условие сходимости. Расходимость гармонического ряда. Признаки сходимости знакоположительных рядов: сравнения, Коши, Даламбера. Доказательство теоремы о том, что признак Коши сильнее признака Даламбера. Интегральный признак Коши. Обобщенный гармонический ряд. Теорема Лейбница о сходимости знакопеременных рядов. Абсолютная и условная сходимость. Формулировка теоремы Римана.

Функциональные ряды. Равномерная сходимость и критерий Коши. Признак Вейерштрасса. Теоремы о предельном переходе (непрерывности), почленном интегрировании и дифференцировании функциональных рядов.

Степенные ряды. Радиус сходимости. Формула Коши - Адамара. Равномерная сходимость и непрерывность суммы степенного ряда, почленное интегрирование и дифференцирование. Достаточное условие разложимости функций в степенные ряды, разложение в ряд Тейлора элементарных функций, область сходимости.

Разложение функций в тригонометрический ряд Фурье. Комплексная форма ряда Фурье, нахождение коэффициентов ряда. Пример: разложение пилообразной функции в ряд Фурье. Предельный переход от ряда Фурье к интегралу Фурье. Преобразование Фурье для производной.

Преобразование компонент трехмерного вектора при вращении системы координат, ортогональность матрицы вращения. Определение тензора n-го ранга. Алгебра тензоров: внешнее произведение, теорема с свертке. Единичный антисимметричный тензор 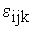(символ Леви-Чивита) и теория детерминантов. Векторное и смешанное произведение векторов как свертка с 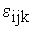. Свойства. Геометрический смысл. Свертка 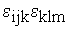и формула В(АС)-С(АВ). Отражение системы координат. Тензоры и псевдотензоры.

Скалярные поля (преобразование, индуцированное инвариантностью). Векторные поля (закон преобразования). Градиент - векторное поле, дивергенция - скалярное поле. Геометрический смысл. Ротор, примеры вычисления.

Криволинейные и поверхностные интегралы II-го рода. Приемы вычисления. Теорема Гаусса. Физический смысл дивергенции. Теорема Стокса. Физический смысл ротора. Три условия потенциальности поля. Ортогональные криволинейные системы координат. Выражения для градиента, дивергенции и лапласиана в криволинейной ортогональной системе координат.

Литература:

1. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Т.1-3,1970.
2. Кудрявцев Л.Д., Математический анализ, т.1-2, 1973.
3. Рудин У. Основы математического анализа, 1975.
4. Будак Б.М., Фомин С.В. Кратные интегралы и ряды, 1967.
5. Сокольников И.С. Тензорный анализ, 1971.
6. Арфкен Г. Математические методы в физике, 1970.
7. Демидович Б.П. Сборник задач по математическому анализу, 1990.
8. Батыгин В.В., Топтыгин Н.Н. Сборник задач по электродинамике, 1970.
9. Мангазеев Б.В., Афанасьев А.Д. Векторный анализ для физиков, методическое пособие, ИГУ, 1992.

Рекомендуемые задачи ([8]):

NN 2546-2552, 2554, 2556-2564, 2568, 2571, 2573, 2574, 2577,2578-2583, 2586-2589, 2589.1, 2593, 26-07-2609, 2619, 2620, 2623,2659-2662, 2664, 2666.1, 2667-2570, 2673, 2675, 2677, 2697,2698,2716, 2717, 2724, 2773Ю, 2745, 2746-2749, 2767-2769, 2774(а-в), 2775, 2792,2812-28-18, 2821-2823, 2831.2, 2833-2835, 2838-2844, 2849, 2851-2857, 2869-2871, 2874, 2879, 2882,2906-2909, 2911, 2912, 2921-2924,2936,2937,2941,2938

Составил доцент Мангазеев Б.В.